Sample Spaces
Problem 0.1
Sara and Megan are two students who show up for a standardized test. Sara has a \(\tfrac{1}{8}\) chance of passing the test, whereas Megan has a \(\tfrac{5}{12}\) chance. What are the chances that at least one of them will pass the test?
Solution. Let \(A\) denote the event that Sara passes the test and \(B\) denote the event that Megan passes. Then we have that \(P(A) = \tfrac{1}{8}\) and \(P(B)=\tfrac{5}{12}\). Now, the probability of at least one of them passing the test is denoted as the union of \(A\) and \(B\), which means
\[ \begin{align} P(A \cup B) & \equiv P(A) + P(B) - P(A \cap B) \\ & \equiv P(A) + P(B) - P(A)P(B) \\ &\equiv \tfrac{1}{8} + \tfrac{5}{12} - \tfrac{1}{8}\times \tfrac{5}{12} \\ &\equiv \tfrac{47}{96} \end{align} \]
Conditional Probability and Bayes’ Rule
Problem 1.1
An email filters spam by scanning commonly occurring words in spam. Suppose that \(70\%\) of email is spam. In \(10\%\) of the spam emails, the expression “fast cash” appears, whereas this phrase only appears in \(1\%\) of non-spam emails. A new email has just arrived, which mentions “fast cash” multiple times. What is the probability that it is indeed spam?
Solution. Let \(S\) be the event that the mail is spam and \(E\) be the event that the mail contains the phrase “fast cash.” We want to find \(P(S|E)\). We have that \(P(E|S) = 0.10\), \(P(E|S^c) = 0.01\), \(P(S) = 0.70\), and \(P(S^c) = 0.30\). By the law of total probability,
\[ \begin{align} P(E) & \equiv P(E|S)P(S) + P(E|S^c)P(S^c) \\ & \equiv 0.10 \times 0.70 + 0.01 \times 0.30 \\ & \equiv 0.073 \end{align} \]
Applying Bayes’ rule, we have
\[ \begin{align} P(S|E) & \equiv \dfrac{P(E|S)P(S)}{P(E)} \\ &\equiv \dfrac{0.10 \times 0.70}{0.073} \\ & \equiv 0.9589 \end{align} \]
Problem 1.2
Companies \(A, B, C\) manufacture screens used for a particular type of computer. The supplied proportions of screens for companies \(A, B, C\) are \(0.5, 0.3, 0.2\), such that \(0.01, 0.02, 0.03\) are defective, respectively. Given that the screen on such a computer is defective, what is the probability that Company \(A\) manufactured it?
Solution. Let \(C_1\) be the event that company \(A\) manufactured the screen and let \(D\) be the event that the screen is defective. We want to find \(P(C_1|D)\). We’re given that \(P(C_1)= 0.5\), \(P(C_2)= 0.3\), \(P(C_3)= 0.2\), \(P(D|C_1) = 0.01\), \(P(D|C_2) = 0.02\), and \(P(D|C_3) = 0.03\). Using Bayes’ rule and the law of total probability:
\[ \begin{align} P(C_1|D) & \equiv \dfrac{P(D|C_1)P(C_1)}{P(D)} \\ & \equiv \dfrac{P(D|C_1)P(C_1)}{P(D|C_1) P(C_1) + P(D|C_2) P(C_2) + P(D|C_3) P(C_3)} \\ & \equiv \dfrac{0.01 \times 0.5}{0.01 \times 0.5 + 0.02\times 0.3 + 0.03 \times 0.2} \\ & \equiv 0.2941176 \end{align} \]
Problem 1.3
A family has \(3\) children, denoted \(A, B, C\). Find the probability that \(A\) is older than \(B\), given that \(A\) is older than \(C\).
Solution. We want to find \(P(A \gt B \,{\mathbf |}\, A \gt C)\). The possible birth orders are \(ABC\), \(ACB\), \(BAC\), \(BCA\), \(CAB\), and \(CBA\). Therefore, we have
\[ \begin{align} P(A \gt B | A \gt C) &\equiv \dfrac{P \left(A\gt B \bigcap A\gt C \right)}{P(A \gt C)} \equiv \dfrac{{1}/{3}}{{1}/{2}} \equiv \frac{2}{3} \end{align} \]
Problem 1.4
Consider an election with candidates \(A\) and \(B\). For a random voter, let \(A\) be the event they voted for \(A\), and \(W\) be the event they’re willing to participate in an exit poll. Suppose that \(P(W|A) = 0.7\) but \(P(W|A^c) = 0.3\). In the exit poll, \(60\%\) of the respondents report they voted for \(A\). Find \(P(A)\), the true percentage of people who voted for \(A\).
Solution. To find \(P(A)\), we use Bayes’ rule to obtain \(P(A|W)\):
\[ \begin{align} P(A | W) & \equiv \dfrac{P(W|A)P(A)}{P(W)} \end{align} \]
Let \(P(A) = p\). We’re given \(P(W|A) = 0.7\) and \(P(A|W) = 0.6\). To obtain \(P(W)\), the probability the voter participates in the exit poll, we use the law of total probability:
\[ \begin{align} P(W) &\equiv P(W|A)P(A) + P(W|A^c)P(A^c) \\ &\equiv 0.7 p + 0.3\times (1-p) \\ &\equiv 0.4p + 0.3 \end{align} \]
Plugging in \(P(W) \equiv 0.4p + 0.3\) into \(P(A|W)\),
\[ \begin{align} P(A | W) & \equiv \dfrac{P(W|A)P(A)}{P(W)} \\ 0.6 & \equiv \dfrac{0.7p}{0.4p + 0.3} \\ 0 &\equiv 0.46p - 0.18 \\ p &\equiv 0.39 \end{align} \]
Hence, the value of \(P(A)\) is \(0.39\).
Problem 1.5
A student answers a multiple-choice problem and must choose one of the \(n\) choices. Let \(K\) be the event in which they know the answer, and \(R\) be the event where they choose the correct answer. Suppose that if they know the correct answer, they’ll get the problem correct. But if they don’t know, they’ll guess. Let \(P(K) = p\). Find \(P(K|R)\) in terms of \(p\) and \(n\).
Solution. We’re given \(P(R|K) =1\). Whereas, if they don’t know the correct answer, they must randomly guess out of the \(n\) choices, i.e., \(P(R|K^c) = \tfrac{1}{n}\). Using Bayes’ Rule and the law of total probability,
\[ \begin{align} P(K|R) &\equiv \dfrac{P(R|K)P(K)}{P(R)} \\ &\equiv \dfrac{p}{P(R|K)P(K) + P(R|K^c)P(K^c)} \\ &\equiv \dfrac{p}{p + \tfrac{1}{n}(1-p)} \\ \end{align} \]
Problem 1.6
There are \(100\) coins in a jar, of which \(99\) are fair and \(1\) is double-ended. Suppose we toss a coin \(7\) times, and all \(7\) times land on \(H\). Find the probability that the coin is double-headed.
Solution. Let \(E\) be the event that the coin lands on \(H\) all \(7\) times and \(D\) be the event that the chosen coin is double-headed. We want to find \(P(D|E)\).
\[ \begin{align} P(D|E) & \equiv \dfrac{P(E|D)P(D)}{P(E)} \\ & \equiv \dfrac{P(E|D)P(D)}{P(E|D)P(D) + P(E|D^c)P(D^c)} \\ & \equiv \dfrac{\tfrac{1}{100}}{\tfrac{1}{100} + \left(\tfrac{1}{2}\right)^7 \cdot \tfrac{99}{100}} \\ &\equiv 0.5638765 \end{align} \]
Discrete Random Variables
Problem 2.1
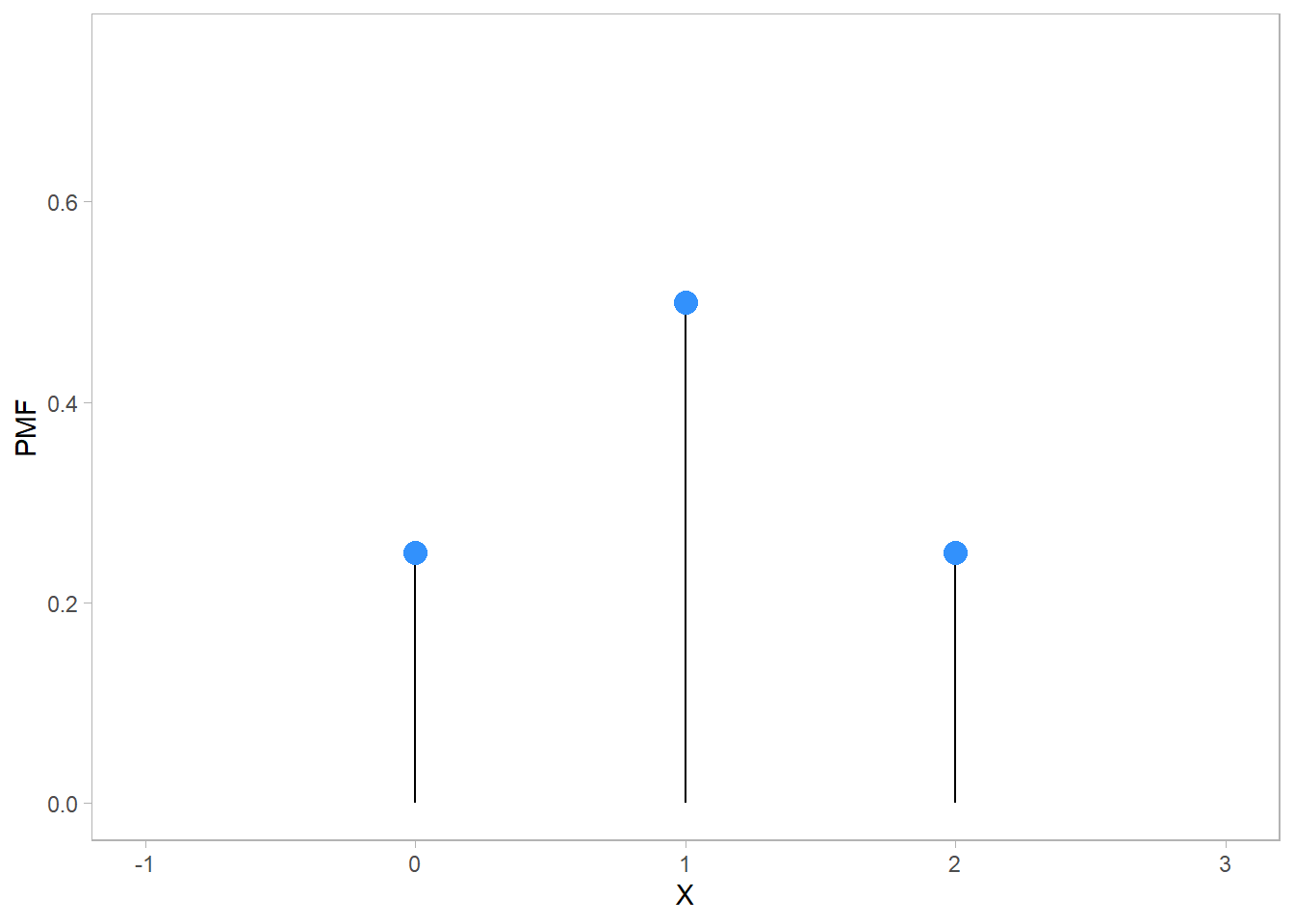
Suppose we toss a fair coin twice. The sample space consists of four possible results: \(\{HH, HT, TH, TT\}\). Let the random variable \(X\) be the number of heads. Find the PMF of \(X\).
Solution. For the random variable \(X\), the possible values are \(0, 1, 2\):
\[ \begin{gather} X(HH) = 2, & X(HT) = X(TH) = 1, & X(TT) = 0 \end{gather} \]
The PMF of \(X\) is the function \(p_X\) given by
\[ \begin{align} p_X(0) & \equiv P(X=0) \equiv \tfrac{1}{4}, \\ p_X(1) & \equiv P(X=1) \equiv \tfrac{1}{2}, \\ p_X(2) & \equiv P(X=2) \equiv \tfrac{1}{4}, \end{align} \]
and \(p_X(x) \equiv 0\) for all other values of \(x\).
Problem 2.2
In a tennis match, the contestants play \(10\) games. In each game, the probability of a player winning is \(0.4\), and the probability of a tie is \(0.6\). Find the probability of exactly \(5\) games ending in a tie.
Solution. Let \(T\) be the number of games ending in a tie. Then \(T\sim \mathrm{Bin}(10,0.6)\), so the PMF is
\[ \begin{align} P(T=t) & \equiv \begin{pmatrix}10 \\ t\end{pmatrix} 0.6^t \cdot 0.4^{n-t} \quad \text{for } t = 0,1,\ldots , n \\ P(T=5) & \equiv \begin{pmatrix}10 \\ 5\end{pmatrix} 0.6^5 \cdot 0.4^{10-5} \\ & \equiv \frac{10!}{5! \cdot 5!}\cdot 0.6^5 \cdot 0.4^5 \cong 0.20 \end{align} \]
Problem 2.3
You have a bag with \(6\) marbles. One marble is red. You draw from the bag \(100\) times, with replacement. What is the probability of drawing a red marble at least once?
Solution. Suppose \(X\) is number of times a red marble is drawn. Then we have \(X \sim \mathrm{Bin}\left(n=6, p=\tfrac{1}{6}\right)\). By the naive definition of probability, this is
\[ \begin{align} \mathbf{P}(X \geq 1) & \equiv 1 - \mathbf{P}(x=0) \\ &\equiv 1 - {\small\begin{pmatrix}100 \\ 0 \end{pmatrix}} \left(\tfrac{1}{6}\right)^{0} \left(\tfrac{5}{6}\right)^{100} \\ & \equiv 1 - \left(\tfrac{5}{6}\right)^{100} \\ & \approx 0.99 \end{align} \]
Exercises from the book Introduction to Probability by Joseph K. Blitzstein and Jessica Hwang © Chapman & Hall/CRC Press, 2014.1